How To Find Potential Energy Of A System
Learning Objectives
By the end of this section, you lot volition exist able to:
- Chronicle the difference of potential energy to piece of work done on a particle for a system without friction or air drag
- Explain the pregnant of the zero of the potential energy function for a system
- Summate and apply the gravitational potential free energy for an object virtually Earth's surface and the elastic potential free energy of a mass-spring system
In Work, we saw that the work done on an object past the constant gravitational forcefulness, almost the surface of Globe, over any deportation is a function but of the difference in the positions of the end-points of the displacement. This property allows us to define a unlike kind of energy for the system than its kinetic energy, which is called potential free energy. We consider diverse properties and types of potential energy in the post-obit subsections.
Potential Energy Basics
In Motion in 2 and Iii Dimensions, nosotros analyzed the motion of a projectile, similar kicking a football in (Effigy). For this example, allow's ignore friction and air resistance. As the football rises, the work done past the gravitational force on the football is negative, because the brawl'south displacement is positive vertically and the force due to gravity is negative vertically. We too noted that the brawl slowed downwards until it reached its highest point in the motion, thereby decreasing the ball's kinetic energy. This loss in kinetic energy translates to a gain in gravitational potential energy of the football game-Earth arrangement.
As the football falls toward Earth, the work done on the football is at present positive, because the displacement and the gravitational force both bespeak vertically downward. The ball too speeds up, which indicates an increase in kinetic energy. Therefore, energy is converted from gravitational potential energy dorsum into kinetic energy.
Based on this scenario, we can define the difference of potential energy from signal A to betoken B as the negative of the work done:
[latex] \text{Δ}{U}_{AB}={U}_{B}-{U}_{A}=\text{−}{W}_{AB}. [/latex]
This formula explicitly states a potential free energy difference, non just an accented potential energy. Therefore, we need to define potential free energy at a given position in such a way as to land standard values of potential energy on their own, rather than potential energy differences. We practise this by rewriting the potential energy function in terms of an arbitrary constant,
[latex] \text{Δ}U=U(\overset{\to }{r})-U({\overset{\to }{r}}_{0}). [/latex]
The selection of the potential free energy at a starting location of [latex] {\overset{\to }{r}}_{0} [/latex] is fabricated out of convenience in the given problem. Most importantly, whatever choice is made should be stated and kept consequent throughout the given problem. There are some well-accepted choices of initial potential energy. For example, the everyman height in a trouble is usually divers as zero potential free energy, or if an object is in infinite, the farthest point away from the system is ofttimes divers as nil potential energy. So, the potential energy, with respect to zero at [latex] {\overset{\to }{r}}_{0}, [/latex] is just [latex] U(\overset{\to }{r}). [/latex]
As long as there is no friction or air resistance, the change in kinetic free energy of the football equals the change in gravitational potential energy of the football. This can be generalized to any potential energy:
[latex] \text{Δ}{K}_{AB}=\text{Δ}{U}_{AB}. [/latex]
Let's look at a specific example, choosing nothing potential energy for gravitational potential energy at convenient points.
Example
Basic Properties of Potential Energy
A particle moves along the x-centrality nether the activeness of a force given by [latex] F=\text{−}a{10}^{two} [/latex], where [latex] a=3\,{\text{Northward/m}}^{ii} [/latex]. (a) What is the difference in its potential free energy as it moves from [latex] {x}_{A}=1\,\text{m} [/latex] to [latex] {x}_{B}=2\,\text{m} [/latex]? (b) What is the particle'due south potential energy at [latex] x=1\,\text{1000} [/latex] with respect to a given 0.five J of potential free energy at [latex] ten=0 [/latex]?
Strategy
(a) The difference in potential energy is the negative of the work washed, every bit defined by (Effigy). The piece of work is defined in the previous chapter as the dot product of the force with the altitude. Since the particle is moving forward in the x-direction, the dot product simplifies to a multiplication ([latex] \lid{i}·\lid{i}=1 [/latex]). To find the total work done, nosotros need to integrate the function between the given limits. Afterwards integration, we can land the piece of work or the potential free energy. (b) The potential free energy part, with respect to cipher at [latex] ten=0 [/latex], is the indefinite integral encountered in part (a), with the constant of integration determined from (Figure). Then, nosotros substitute the x-value into the part of potential energy to calculate the potential energy at [latex] x=1\,\text{thou}. [/latex]
Solution
- The work done by the given force as the particle moves from coordinate x to [latex] x+dx [/latex] in i dimension is
[latex] dW=\overset{\to }{F}·d\overset{\to }{r}=Fdx=\text{−}a{x}^{2}dx. [/latex]
Substituting this expression into (Figure), we obtain
[latex] \text{Δ}U=\text{−}Due west=\underset{{x}_{1}}{\overset{{x}_{2}}{\int }}a{x}^{2}dx=\frac{1}{3}(iii\,{\text{N/m}}^{2}){{x}^{2}|}_{1\,\text{one thousand}}^{2\,\text{g}}=7\,\text{J}. [/latex]
- The indefinite integral for the potential energy function in part (a) is
[latex] U(x)=\frac{1}{3}a{x}^{three}+\text{const}., [/latex]
and we desire the abiding to be determined by
[latex] U(0)=0.5\,\text{J}. [/latex]
Thus, the potential energy with respect to zilch at [latex] 10=0 [/latex] is just
[latex] U(x)=\frac{1}{3}a{ten}^{3}+0.5\,\text{J}. [/latex]
Therefore, the potential energy at [latex] ten=1\,\text{m} [/latex] is
[latex] U(1\,\text{m})=\frac{one}{3}(three\,{\text{N/m}}^{2}){(ane\,\text{m})}^{3}+0.5\,\text{J}=ane.v\,\text{J}. [/latex]
Significance
In this one-dimensional example, any role we tin integrate, contained of path, is bourgeois. Notice how we applied the definition of potential energy difference to decide the potential energy function with respect to cypher at a called point. Also notice that the potential free energy, every bit adamant in part (b), at [latex] x=ane\,\text{m} [/latex] is [latex] U(1\,\text{chiliad})=ane\,\text{J} [/latex] and at [latex] x=2\,\text{thou} [/latex] is [latex] U(2\,\text{thou})=8\,\text{J} [/latex]; their divergence is the result in part (a).
Bank check Your Understanding
In (Figure), what are the potential energies of the particle at [latex] x=i\,\text{m} [/latex] and [latex] x=2\,\text{1000} [/latex] with respect to zero at [latex] ten=i.five\,\text{one thousand} [/latex]? Verify that the deviation of potential energy is still 7 J.
Show Solution
[latex] (4.63\,\text{J})-(-2.38\,\text{J})=7.00\,\text{J} [/latex]
Systems of Several Particles
In general, a system of interest could consist of several particles. The departure in the potential energy of the system is the negative of the piece of work done past gravitational or elastic forces, which, as we volition meet in the next section, are bourgeois forces. The potential energy difference depends only on the initial and final positions of the particles, and on some parameters that characterize the interaction (similar mass for gravity or the leap constant for a Hooke's law force).
It is of import to call up that potential free energy is a property of the interactions between objects in a chosen arrangement, and not but a property of each object. This is especially true for electric forces, although in the examples of potential energy we consider beneath, parts of the system are either so big (similar Earth, compared to an object on its surface) or so small (like a massless spring), that the changes those parts undergo are negligible if included in the system.
Types of Potential Energy
For each type of interaction present in a organization, y'all tin can characterization a corresponding type of potential energy. The total potential energy of the system is the sum of the potential energies of all the types. (This follows from the additive property of the dot production in the expression for the piece of work done.) Allow'southward look at some specific examples of types of potential energy discussed in Work. Showtime, nosotros consider each of these forces when acting separately, and then when both act together.
Gravitational potential energy near Earth's surface
The system of involvement consists of our planet, Globe, and 1 or more particles nigh its surface (or bodies small plenty to exist considered every bit particles, compared to World). The gravitational force on each particle (or torso) is simply its weight mg well-nigh the surface of World, acting vertically down. Co-ordinate to Newton'south third law, each particle exerts a force on Earth of equal magnitude but in the opposite direction. Newton's second law tells us that the magnitude of the dispatch produced past each of these forces on Earth is mg divided by Earth'due south mass. Since the ratio of the mass of any ordinary object to the mass of Earth is vanishingly pocket-size, the motion of Earth can be completely neglected. Therefore, we consider this system to exist a group of single-particle systems, subject area to the uniform gravitational strength of Earth.
In Piece of work, the work done on a body by Earth'due south uniform gravitational force, about its surface, depended on the mass of the body, the acceleration due to gravity, and the difference in superlative the torso traversed, equally given by (Figure). Past definition, this piece of work is the negative of the deviation in the gravitational potential energy, and then that departure is
[latex] \text{Δ}{U}_{\text{grav}}=\text{−}{W}_{\text{grav},AB}=mg({y}_{B}-{y}_{A}). [/latex]
Yous can see from this that the gravitational potential energy function, near Earth's surface, is
[latex] U(y)=mgy+\text{const}. [/latex]
You can choose the value of the constant, every bit described in the discussion of (Figure); yet, for solving most problems, the about convenient abiding to choose is zero for when [latex] y=0, [/latex] which is the lowest vertical position in the trouble.

Don't jump—you have then much potential (gravitational potential energy, that is). (credit: Andy Spearing)
Example
Gravitational Potential Energy of a Hiker
The summit of Great Blueish Loma in Milton, MA, is 147 m above its base of operations and has an elevation above sea level of 195 thousand ((Figure)). (Its Native American name, Massachusett, was adopted by settlers for naming the Bay Colony and country near its location.) A 75-kg hiker ascends from the base to the summit. What is the gravitational potential energy of the hiker-Earth system with respect to zero gravitational potential free energy at base acme, when the hiker is (a) at the base of operations of the colina, (b) at the acme, and (c) at sea level, afterward?

Figure eight.3 Sketch of the profile of Cracking Blueish Colina, Milton, MA. The altitudes of the three levels are indicated.
Strategy
Start, we demand to selection an origin for the y-axis and then determine the value of the constant that makes the potential free energy zero at the height of the base. Then, we tin determine the potential energies from (Figure), based on the human relationship betwixt the zero potential energy acme and the summit at which the hiker is located.
Solution
- Allow's choose the origin for the y-axis at base height, where nosotros also want the zero of potential energy to exist. This choice makes the abiding equal to nothing and
[latex] U(\text{base})=U(0)=0. [/latex]
- At the acme, [latex] y=147\,\text{one thousand} [/latex], so
[latex] U(\text{summit})=U(147\,\text{m})=mgh=(75\,×\,9.8\,\text{N})(147\,\text{thousand})=108\,\text{kJ}. [/latex]
- At ocean level, [latex] y=(147-195)\text{m}=-48\,\text{m} [/latex], and so
[latex] U(\text{sea-level})=(75\,×\,9.8\,\text{N})(-48\,\text{k})=-35.iii\,\text{kJ}. [/latex]
Significance
Besides illustrating the use of (Figure) and (Figure), the values of gravitational potential energy nosotros found are reasonable. The gravitational potential energy is higher at the summit than at the base of operations, and lower at sea level than at the base. Gravity does piece of work on y'all on your manner upwards, too! It does negative work and not quite as much (in magnitude), as your muscles practise. But information technology certainly does work. Similarly, your muscles practise work on your fashion down, as negative piece of work. The numerical values of the potential energies depend on the choice of zero of potential energy, but the physically meaningful differences of potential energy do not. [Annotation that since (Figure) is a difference, the numerical values do not depend on the origin of coordinates.]
Check Your Understanding What are the values of the gravitational potential free energy of the hiker at the base, summit, and ocean level, with respect to a sea-level goose egg of potential energy?
Show Solution
35.3 kJ, 143 kJ, 0
Elastic potential energy
In Work, we saw that the work done past a perfectly elastic leap, in one dimension, depends only on the spring abiding and the squares of the displacements from the unstretched position, as given in (Effigy). This work involves merely the backdrop of a Hooke's police interaction and non the backdrop of real springs and any objects are attached to them. Therefore, we can ascertain the difference of elastic potential energy for a spring strength equally the negative of the work done past the leap force in this equation, before nosotros consider systems that embody this type of force. Thus,
[latex] \text{Δ}U=\text{−}{Westward}_{AB}=\frac{one}{ii}grand({x}_{B}^{2}-{x}_{A}^{2}), [/latex]
where the object travels from betoken A to point B. The potential energy function corresponding to this difference is
[latex] U(ten)=\frac{1}{2}k{ten}^{2}+\text{const}. [/latex]
If the spring force is the just force acting, it is simplest to accept the zero of potential energy at [latex] x=0 [/latex], when the spring is at its unstretched length. Then, the constant is (Figure) is zero. (Other choices may be more convenient if other forces are acting.)
Example
Spring Potential Free energy
A system contains a perfectly rubberband spring, with an unstretched length of 20 cm and a spring abiding of 4 North/cm. (a) How much elastic potential energy does the jump contribute when its length is 23 cm? (b) How much more potential energy does it contribute if its length increases to 26 cm?
Strategy
When the spring is at its unstretched length, information technology contributes nothing to the potential energy of the system, and then we tin can use (Figure) with the constant equal to zero. The value of x is the length minus the unstretched length. When the jump is expanded, the spring's displacement or deviation betwixt its relaxed length and stretched length should be used for the 10-value in computing the potential energy of the bound.
Solution
- The deportation of the spring is [latex] x=23\,\text{cm}-20\,\text{cm}=3\,\text{cm} [/latex], so the contributed potential energy is [latex] U=\frac{1}{ii}k{x}^{2}=\frac{i}{ii}(iv\,\text{N/cm}){(3\,\text{cm})}^{ii}=0.18\,\text{J} [/latex].
- When the leap's displacement is [latex] x=26\,\text{cm}-20\,\text{cm}=half dozen\,\text{cm} [/latex], the potential energy is [latex] U=\frac{one}{2}m{x}^{2}=\frac{1}{ii}(4\,\text{Due north/cm}){(6\,\text{cm})}^{2}=0.72\,\text{J} [/latex], which is a 0.54-J increase over the amount in function (a).
Significance
Calculating the elastic potential free energy and potential energy differences from (Effigy) involves solving for the potential energies based on the given lengths of the spring. Since U depends on [latex] {x}^{two} [/latex], the potential energy for a compression (negative 10) is the aforementioned as for an extension of equal magnitude.
Cheque Your Understanding
When the length of the spring in (Figure) changes from an initial value of 22.0 cm to a concluding value, the elastic potential free energy it contributes changes by [latex] -0.0800\,\text{J}. [/latex] Detect the last length.
Show Solution
22.8 cm. Using 0.02 m for the initial displacement of the spring (see higher up), nosotros calculate the terminal displacement of the spring to be 0.028 one thousand; therefore the length of the spring is the unstretched length plus the deportation, or 22.viii cm.
Gravitational and elastic potential energy
A unproblematic system embodying both gravitational and elastic types of potential energy is a i-dimensional, vertical mass-spring system . This consists of a massive particle (or block), hung from ane end of a perfectly elastic, massless spring, the other terminate of which is stock-still, as illustrated in (Effigy).
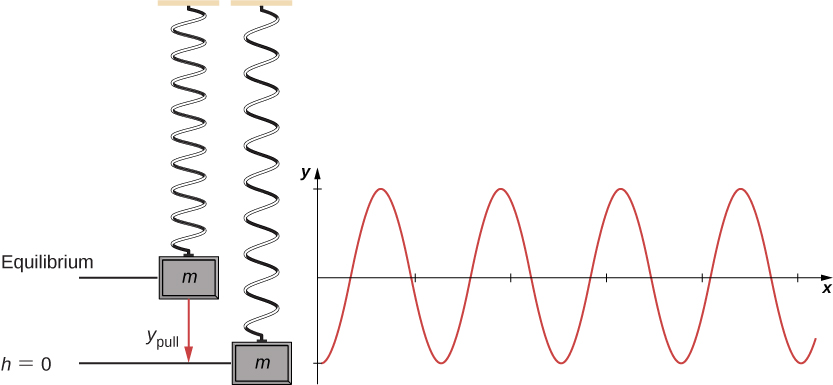
Figure eight.four A vertical mass-spring system, with the y-axis pointing upwards. The mass is initially at an equilibrium position and pulled downwardly to [latex] {y}_{\text{pull}}. [/latex] An oscillation begins, centered at the equilibrium position.
Commencement, allow's consider the potential energy of the system. Assuming the bound is massless, the system of the block and Earth gains and loses potential free energy. Nosotros need to define the abiding in the potential free energy office of (Figure). Often, the ground is a suitable pick for when the gravitational potential free energy is null; however, in this case, the lowest point or when [latex] h=0 [/latex] is a convenient location for zero gravitational potential energy. Note that this pick is capricious, and the problem can exist solved correctly even if another selection is picked.
We must also define the elastic potential free energy of the system and the corresponding abiding, as detailed in (Effigy). The equilibrium location is the most suitable mathematically to cull for where the potential free energy of the spring is cypher.
Therefore, based on this convention, each potential energy and kinetic energy can be written out for three critical points of the organization: (one) the lowest pulled point, (2) the equilibrium position of the spring, and (three) the highest point achieved. We note that the total energy of the system is conserved, so whatsoever total energy in this chart could be matched up to solve for an unknown quantity. The results are shown in (Figure).
| Gravitational P.E. | Elastic P.Due east. | Kinetic E. | |
|---|---|---|---|
| (3) Highest Point | [latex] 2mg{y}_{\text{pull}} [/latex] | [latex] \frac{1}{2}grand{y}^{two}{}_{\text{pull}} [/latex] | [latex] 0 [/latex] |
| (2) Equilibrium | [latex] mg{y}_{\text{pull}} [/latex] | [latex] 0 [/latex] | [latex] \frac{i}{2}thousand{v}^{ii} [/latex] |
| (1) Everyman Point | [latex] 0 [/latex] | [latex] \frac{i}{two}1000{y}^{2}{}_{\text{pull}} [/latex] | [latex] 0 [/latex] |

Figure 8.5 A bungee jumper transforms gravitational potential energy at the start of the jump into elastic potential energy at the bottom of the jump.
Example
Potential Energy of a Vertical Mass-Spring System
A block weighing [latex] 12\,\text{N} [/latex] is hung from a spring with a spring constant of [latex] half-dozen.0\,\text{N}\text{/}\text{chiliad} [/latex], as shown in (Figure). The block is pulled downwardly an additional [latex] v.0\,\text{cm} [/latex] from its equilibrium position and released. (a) What is the departure in just the jump potential free energy, from an initial equilibrium position to its pulled-downward position? (b) What is the deviation in only the gravitational potential free energy from its initial equilibrium position to its pulled-downwardly position? (c) What is the kinetic energy of the block as it passes through the equilibrium position from its pulled-down position?
Strategy
In parts (a) and (b), we want to detect a difference in potential energy, so we can employ (Figure) and (Figure), respectively. Each of these expressions takes into consideration the change in the energy relative to some other position, farther emphasizing that potential energy is calculated with a reference or second point in listen. By choosing the conventions of the lowest point in the diagram where the gravitational potential energy is zip and the equilibrium position of the jump where the elastic potential free energy is zero, these differences in energies tin now be calculated. In part (c), we accept a look at the differences between the two potential energies. The difference between the two results in kinetic free energy, since in that location is no friction or drag in this organization that tin can accept energy from the system.
Solution
- Since the gravitational potential energy is zero at the lowest point, the change in gravitational potential energy is
[latex] \text{Δ}{U}_{\text{grav}}=mgy-0=(12\,\text{Northward})(5.0\,\text{cm})=0.sixty\,\text{J}. [/latex]
- The equilibrium position of the spring is defined as goose egg potential energy. Therefore, the change in rubberband potential energy is
[latex] \text{Δ}{U}_{\text{elastic}}=0-\frac{1}{ii}one thousand{y}_{\text{pull}}^{2}=\text{−}(\frac{1}{2})(6.0\frac{\text{N}}{\text{grand}}){(five.0\,\text{cm})}^{2}=-0.75\,\text{J}. [/latex]
- The block started off existence pulled downward with a relative potential energy of [latex] 0.75\,\text{J}. [/latex] The gravitational potential energy required to ascension [latex] 5.0\,\text{cm is}\,0.60\,\text{J} [/latex]. The energy remaining at this equilibrium position must exist kinetic energy. We can solve for this gain in kinetic energy from (Figure),
[latex] \text{Δ}K=\text{−}(\text{Δ}{U}_{\text{elastic}}+\text{Δ}{U}_{\text{grav}})=\text{−}(-0.75\,\text{J}+0.lx\,\text{J})=0.15\,\text{J}. [/latex]
Significance
Fifty-fifty though the potential energies are relative to a chosen cipher location, the solutions to this problem would be the same if the zero energy points were chosen at different locations.
Check Your Agreement
Suppose the mass in (Figure) is in equilibrium, and you pull information technology down another three.0 cm, making the pulled-down distance a total of [latex] eight.0\,\text{cm}. [/latex] The elastic potential free energy of the bound increases, because you're stretching it more than, simply the gravitational potential energy of the mass decreases, because you lot're lowering it. Does the total potential energy increment, decrease, or remain the aforementioned?
Prove Solution
It increases because yous had to exert a downward force, doing positive work, to pull the mass downwards, and that's equal to the modify in the full potential energy.
View this simulation to learn about conservation of energy with a skater! Build tracks, ramps and jumps for the skater and view the kinetic energy, potential free energy and friction every bit he moves. You tin can also take the skater to different planets or even space!
A sample chart of a multifariousness of energies is shown in (Effigy) to requite y'all an idea about typical energy values associated with certain events. Some of these are calculated using kinetic free energy, whereas others are calculated by using quantities found in a form of potential energy that may not have been discussed at this point.
| Object/phenomenon | Free energy in joules |
|---|---|
| Big Bang | [latex] {10}^{68} [/latex] |
| Almanac world energy utilisation | [latex] 4.0\,×\,{ten}^{20} [/latex] |
| Big fusion bomb (9 megaton) | [latex] 3.viii\,×\,{10}^{16} [/latex] |
| Hiroshima-size fission flop (10 kiloton) | [latex] four.2\,×\,{10}^{13} [/latex] |
| ane barrel crude oil | [latex] 5.ix\,×\,{10}^{ix} [/latex] |
| 1 ton TNT | [latex] 4.ii\,×\,{10}^{9} [/latex] |
| i gallon of gasoline | [latex] 1.2\,×\,{10}^{8} [/latex] |
| Daily adult food intake (recommended) | [latex] ane.2\,×\,{10}^{vii} [/latex] |
| 1000-kg motorcar at 90 km/h | [latex] 3.1\,×\,{10}^{v} [/latex] |
| Tennis brawl at 100 km/h | [latex] 22 [/latex] |
| Mosquito [latex] ({x}^{-ii}\,\text{g at 0.5 m/south}) [/latex] | [latex] 1.iii\,×\,{10}^{-6} [/latex] |
| Single electron in a Tv tube beam | [latex] 4.0\,×\,{10}^{-fifteen} [/latex] |
| Energy to intermission one Deoxyribonucleic acid strand | [latex] {x}^{-19} [/latex] |
Summary
- For a single-particle arrangement, the difference of potential free energy is the opposite of the work done past the forces interim on the particle as it moves from ane position to another.
- Since merely differences of potential energy are physically meaningful, the nada of the potential energy function can exist chosen at a convenient location.
- The potential energies for Earth'southward abiding gravity, near its surface, and for a Hooke'due south law force are linear and quadratic functions of position, respectively.
Conceptual Questions
The kinetic energy of a system must always exist positive or nada. Explicate whether this is true for the potential free energy of a organization.
Evidence Solution
The potential energy of a system can exist negative because its value is relative to a divers signal.
The strength exerted by a diving lath is conservative, provided the internal friction is negligible. Assuming friction is negligible, describe changes in the potential energy of a diving board as a swimmer drives from it, starting just before the swimmer steps on the board until simply later on his feet get out information technology.
Describe the gravitational potential energy transfers and transformations for a javelin, starting from the point at which an athlete picks up the javelin and ending when the javelin is stuck into the ground after being thrown.
Show Solution
If the reference bespeak of the footing is null gravitational potential energy, the javelin beginning increases its gravitational potential free energy, followed by a decrease in its gravitational potential energy as it is thrown until it hits the ground. The overall change in gravitational potential energy of the javelin is nil unless the center of mass of the javelin is lower than from where it is initially thrown, and therefore would have slightly less gravitational potential energy.
A couple of soccer balls of equal mass are kicked off the ground at the same speed but at dissimilar angles. Soccer ball A is kicked off at an angle slightly in a higher place the horizontal, whereas brawl B is kicked slightly below the vertical. How do each of the post-obit compare for ball A and ball B? (a) The initial kinetic energy and (b) the change in gravitational potential energy from the ground to the highest point? If the energy in role (a) differs from part (b), explain why at that place is a difference between the ii energies.
What is the dominant gene that affects the speed of an object that started from balance downwards a frictionless incline if the only piece of work done on the object is from gravitational forces?
Testify Solution
the vertical height from the ground to the object
Two people observe a leaf falling from a tree. One person is standing on a ladder and the other is on the ground. If each person were to compare the energy of the leafage observed, would each person detect the following to be the same or different for the leaf, from the bespeak where it falls off the tree to when it hits the ground: (a) the kinetic free energy of the leaf; (b) the change in gravitational potential energy; (c) the final gravitational potential energy?
Issues
Using values from (Figure), how many Deoxyribonucleic acid molecules could exist broken by the free energy carried by a single electron in the beam of an sometime-fashioned Television tube? (These electrons were non unsafe in themselves, just they did create unsafe X-rays. Later-model tube TVs had shielding that captivated 10-rays before they escaped and exposed viewers.)
If the free energy in fusion bombs were used to supply the free energy needs of the world, how many of the 9-megaton diversity would be needed for a year'due south supply of energy (using data from (Figure))?
A camera weighing ten Due north falls from a small drone hovering [latex] 20\,\text{m} [/latex] overhead and enters free fall. What is the gravitational potential energy change of the camera from the drone to the ground if you take a reference indicate of (a) the basis existence naught gravitational potential energy? (b) The drone being zero gravitational potential free energy? What is the gravitational potential energy of the camera (c) before information technology falls from the drone and (d) after the camera lands on the basis if the reference indicate of nothing gravitational potential energy is taken to be a second person looking out of a building [latex] thirty\,\text{grand} [/latex] from the ground?
Show Solution
[latex] \text{a.}\,-200\,\text{J};\,\text{b.}\,-200\,\text{J};\,\text{c.}\,-100\,\text{J};\,\text{d.}\,-300\,\text{J} [/latex]
Someone drops a [latex] 50-\text{g} [/latex] pebble off of a docked prowl send, [latex] seventy.0\,\text{thousand} [/latex] from the h2o line. A person on a dock [latex] 3.0\,\text{thousand} [/latex] from the water line holds out a net to catch the pebble. (a) How much piece of work is washed on the pebble by gravity during the drib? (b) What is the alter in the gravitational potential energy during the drib? If the gravitational potential energy is zero at the h2o line, what is the gravitational potential energy (c) when the pebble is dropped? (d) When it reaches the net? What if the gravitational potential energy was [latex] 30.0 [/latex] Joules at water level? (east) Find the answers to the aforementioned questions in (c) and (d).
A cat's crinkle brawl toy of mass [latex] fifteen\,\text{yard} [/latex] is thrown straight up with an initial speed of [latex] 3\,\text{g/southward} [/latex]. Assume in this problem that air drag is negligible. (a) What is the kinetic energy of the ball as it leaves the manus? (b) How much work is washed by the gravitational force during the ball'southward rise to its peak? (c) What is the alter in the gravitational potential energy of the brawl during the rise to its peak? (d) If the gravitational potential energy is taken to exist zero at the point where it leaves your hand, what is the gravitational potential energy when it reaches the maximum height? (e) What if the gravitational potential free energy is taken to exist cipher at the maximum height the ball reaches, what would the gravitational potential energy exist when it leaves the paw? (f) What is the maximum superlative the ball reaches?
Show Solution
[latex] \text{a.}\,0.068\,\text{J};\,\text{b.}\,-0.068\,\text{J};\,\text{c.}\,0.068\,\text{J};\,\text{d.}\,0.068\,\text{J};\,\text{eastward.}\,-0.068\,\text{J};\,\text{f.}\,46\,\text{cm} [/latex]
Glossary
- potential energy
- part of position, energy possessed by an object relative to the organisation considered
- potential energy departure
- negative of the work washed acting between ii points in space
Source: https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/8-1-potential-energy-of-a-system/
Posted by: freeseterent93.blogspot.com


0 Response to "How To Find Potential Energy Of A System"
Post a Comment